いずれ実現された暁には異次元の計算速度を誇るとされる「量子コンピュータ」は、そのアイディアが有名なファイマン博士によって発案された1981年から長年に渡って、一部の物理学者らの好奇心に駆られた半ば学術的研究の対象に過ぎなかった。
そこから米マイクロソフトなど巨大メーカーにおける、実用化を目指した本格的な開発段階へと移行したのは、「標準的な電子工学の技術や材料で量子ビットを作れる」と判明した2000年代後半のことであった(連載第2回「量子コンピュータの黎明期を振り返る」を参照)。
当時、研究開発が進められた量子コンピュータは、英国の物理学者デイヴィッド・ドイッチュ博士が考案した「量子ゲート」と呼ばれる方式に基づいていた。これは従来型コンピュータの演算素子である「ゲート(論理回路)」を量子計算用に改造した方式だ。
現代コンピュータの「ゲート」とは
最初に少し回り道になるが、この「ゲート」と、それをベースとする現代コンピュータの基本原理について簡単に説明しておこう。
パソコンからスパコンまで現在広く使われている汎用デジタル・コンピュータは、いわゆる「ブール代数」に基づいて計算を実行している。ブール代数は19世紀に活躍した英国の数学者ジョージ・ブールが開拓したもので、「真(1)」と「偽(0)」という2つの値だけで、この世界の全論理を記述する学問だ。
このブール代数を、コンピュータの基本的な演算素子(部品)に転化したものが「ゲート(論理回路)」である。それらは二進数・算術演算の掛け算に相似するAND回路、同じく足し算に相似するOR回路、さらに二進数の1と0を反転させるNOT回路等から構成される(図1)。
これら各種ゲートを数限りなく組み合わせること(図2)によって、汎用コンピュータは極めて複雑で高度な演算(計算)を行い、現代社会における様々な情報処理をこなすことができるのだ。
これらのゲート(論理回路)は、物理的には「トランジスタ」と呼ばれる電子部品から作られる。このトランジスタを微細化して何千万~何十億個も半導体の基盤上に集積したものが「LSI(大規模集積回路)」、つまり現代コンピュータの演算処理などを担う主要部品だ(図3)。
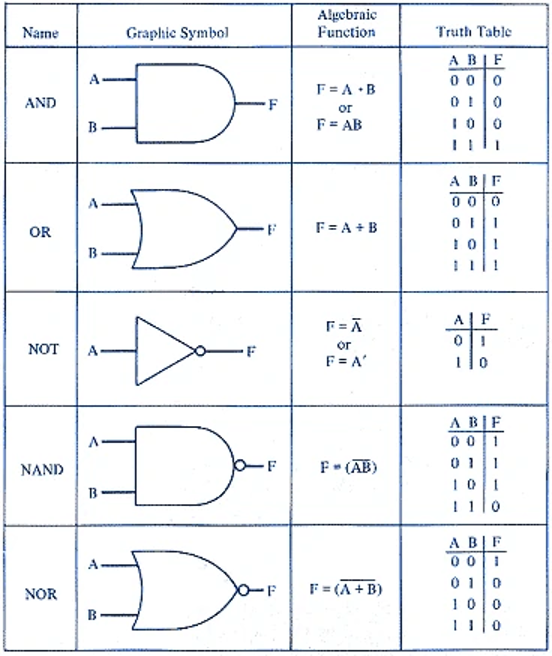
出典:https://bmet.fandom.com/wiki/Logic_Gates
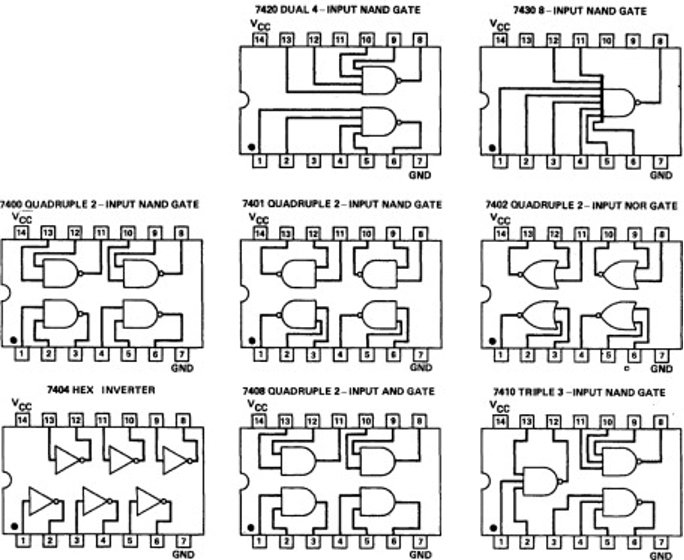
出典:https://www.sciencedirect.com/topics/engineering/digital-integrated-circuits

出典:https://sciencing.com/learn-microprocessor-programming-7483604.html
量子ゲートとは何か
さて前置きが長くなったが、本稿の主題である「量子ゲート」とは、以上のようなゲートを量子計算の基本原理である「量子並列性」に合わせて改造したもので、数学的には「行列(Matrix)」によって表現される(図4)。
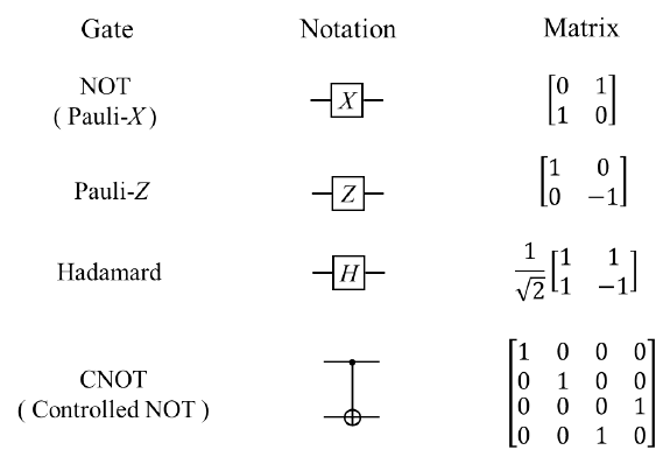
出典:https://www.researchgate.net/figure/Commonly-used-quantum-gates-NOT-Z-Hadamard-and-CNOT_fig1_266855738
量子ゲート(図4)は従来のゲート(図1)を改造したものだと言うが、図1と図4とでは呼称も表記法も全然違うではないか!―― そんな苦情が聞こえてきそうだが、確かに、その点は認めざるを得ない。しかも「行列」つまり「線形代数」という高等数学まで使っているので、プロの自然科学者ならとにかく、一般の人たちが量子ゲートを腹の底から理解するのは困難だ。
その点はご容赦頂くとして、多少なりとも直観的に理解することは可能ではないかと思われる。
まず量子ゲートが数学的には単なる掛け算や足し算ではなく、それらを組み合わせた行列で表現される理由は、量子ゲートの演算対象となる量子ビットが0と1の重ね合わせによって表現されるからだ。それは量子力学の表記法に従って:
α|0> + β|1>
のような数式で表される。
これまでの連載で「量子ビットは同時に0と1の両方の状態を取り得る」と繰り返し説明してきたが、それを数学的に表現したのが、この式だ。因みに|0>や|1>は単なる数字(スカラー)ではなく、次元を有するベクトルだが、本稿ではそこまで厳密な説明は手に余るので、直観的には数字の0や1と思って頂いて構わない。
量子ゲートが行う演算の様子
このような量子ビットを量子ゲート(行列)で処理する演算の様子は、以下の図5に示されている。
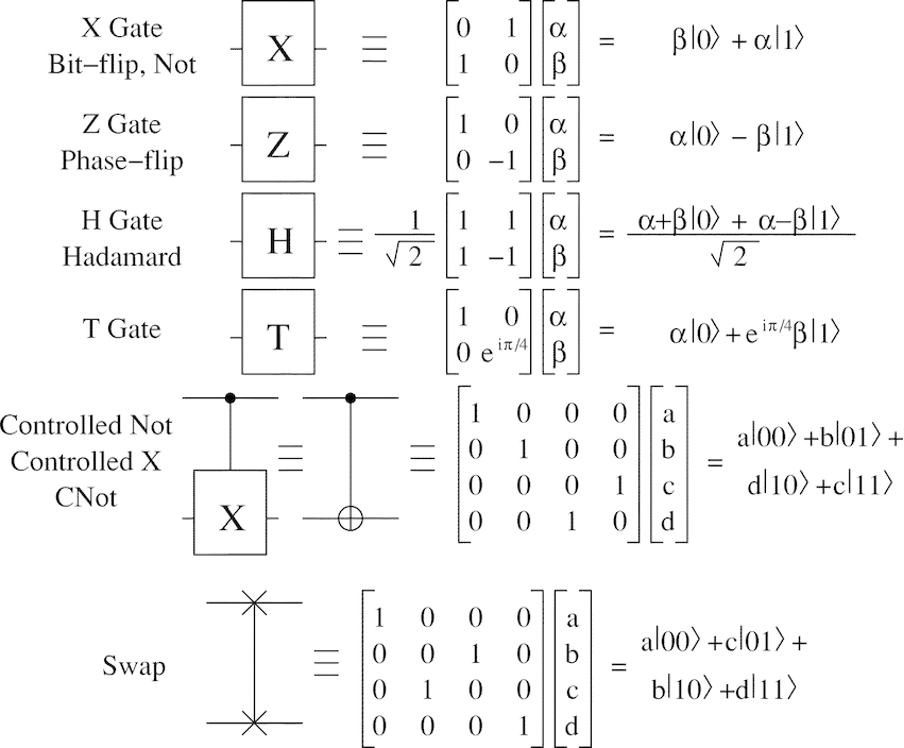
出典:https://www.researchgate.net/figure/Basic-quantum-gates-and-their-matrix-representations_fig1_3409658
いきなり、こんなミステリアスな計算の様子を見せられても正直困惑されるだろうが、ここではその内容を理解するのではなく、あくまでイメージとして視覚的に把握して頂ければ十分だ。
これら量子ゲートによる論理演算は、図1に示した従来型コンピュータのゲートによる論理演算と比喩的には対応している。しかし実際には、ブール代数に従う従来型ゲートの論理演算が「掛け算」や「足し算」など単純な算術計算と相似形を為していたのに対し、量子ゲートの論理演算はそれよりもずっと複雑であることがイメージとしてご理解頂けたと思う。
もちろん中には、量子ビットの0と1を反転させるXGate(NOT)のように、従来型のゲート(NOT)に上手く対応するものもあるが、それ以外のケースでは従来型ゲートよりも遥かに複雑な演算をこなさねばならない。このような複雑さは、単なる0か1かではなく、0と1の重ね合わせを表現する量子ビットを相手にした論理演算である以上、止むを得ない。
たとえミステリアスで複雑でも、これら量子ゲートによる論理演算を、同時に(2のn乗)個の状態を取り得るn量子ビットに適用すれば、量子並列性に従って桁外れに高速な汎用計算を実現できることになる(連載第2回を参照)。これが量子コンピュータの基本的な原理である。
量子ゲートは不安定で壊れ易い
本稿の冒頭でも紹介したように、量子ゲートは、1985年に世界で初めて英国の物理学者、デイヴィッド・ドイッチュ博士が量子コンピュータの原理として提唱した方式である。以来、日米欧をはじめ世界中で研究されてきた量子コンピュータの大多数が、この「量子ゲート」方式に基づいていた。言わば、量子コンピュータ開発の主流方式である。
しかし、その開発の歩みは遅かった。今世紀に入ってIBMやHP(ヒューレット・パッカード)などが量子ゲート方式の基礎技術を確立したとされるが、いずれも実験室レベルに止まり、そこで作られた”量子コンピュータ”は(連載第2回で紹介した)「15を3と5に素因数分解する」程度の極めて初歩的な計算しか出来なかった。
この点は、2000年代後半に手頃な素材や技術で量子コンピュータが作れそうだと分かってからも大して変わらなかった。
この頃になっても、未だ量子ビット数はせいぜい7、8個のレベルに止まっていた。量子ゲート方式は外部ノイズの影響を受け易く、量子ビットを一旦作る事が出来ても、すぐに壊れてしまう。これが量子ビット数を思うように増やす事が出来なかった主な理由だ。
現実世界の問題を解決する量子コンピュータを実現するには、最低でも数百万個の量子ビットが必要と考えられていた。従って、本格的な量子コンピュータが登場するのは何十年も先になると当時は見られていた。
この予想を覆そうとしたのが、次回の連載コラムで紹介するカナダのD-Waveである。
(次回へ続く)
KDDI総合研究所リサーチフェロー 小林 雅一
